Kapitel 13: Chemisches Rechnen

 

Formelspickzettel

n = m/M

c = n/V

ρ = m/V

Vm = V/n

m/M = V/Vm

 

Für die Oberstufe:

p · V = n · R_m · T

k = A · e ^{(-E_A / R·T)}

 

Die Masse von Atomen und Molekülen

Kannst Du Dich noch an das Gesetz der vielfachen Massenverhältnisse erinnern? Wenn nicht, wiederhole kurz das entsprechende Kapitel.

 

Zur Erinnerung: Aussagen einer chemischen Formel:

FeS : 1 Atom Eisen reagiert mit einem Atom Schwefel

FeS₂ : 1 Atom Eisen reagiert mit zwei Atomen Schwefel

Der Index hinter den Elementsymbolen gibt das Zahlenverhältnis der Atome in der Formel zueinander an.

=> Die Masse steht immer im Verhältnis zur Anzahl der Atome, da diese nicht teilbar sind!

=> In 7g Fe sind genauso viele Atome wie in 4g Schwefel.

 

Diese Betrachtungen haben wir bisher immer auf eines oder wenige Atome bezogen. Auch in Reaktionsgleichungen hat man bisher immer mit geringen Anzahlen an Atomen gearbeitet. Da aber in der Natur nur sehr selten einzelne Atome vorkommen, sondern in der Regel sehr sehr viele, benötigt man zum praktischen Umgang mit Atomen ein neues Hilfsmittel zur Vereinfachung und vor allem zu praktischen Berechnung.

 

a) Die Avogadro Zahl

Der Chemiker Avogadro¹ erkannte als erster das Problem, dass die sehr kleinen Atome schon in sehr geringen Stoffportionen in sehr hoher Anzahl vorliegen. Denn oft ist es im Laboralltag oder bei der Erforschung von unbekannten Stoffen nötig zu wissen, wie viele Teilchen in einer bestimmten Stoffportion vorhanden sind. Aber natürlich sind die Teilchenmengen zum Abzählen viel zu groß.

Avogadro benötige eine Zahl, um diese großen Mengen von Atomen beschreiben zu können und um schließlich damit auch rechnen zu können (ohne dabei Zahlen mit mehr als 20 Nullen notieren zu müssen).

Auf dem Markt hatte er beobachtet, dass 12 Eier zu einem Dutzend zusammengefasst werden. Menschen haben so etwas schon immer gemacht, so ist zum Beispiel auch die Mengenangabe „Dutzend“ für 12 Teilchen entstanden. Konnte er einen ähnlichen Trick für Atome benutzen?

Er fasste zur Vereinfachung die großen Anzahlmengen der Atome zu einer kleineren Zahl zusammen und nannte diese dann Stoffmenge (mit der Einheit „mol“).

 

Avogadro legte fest: 1 mol entspricht 6,022·10²³ Atomen (=602 200 000 000 000 000 000 000 Atome)

1 mol ist die Stoffportion in der 6,022 · 10²³ Teilchen enthalten sind.

Die Stoffmenge wird mit dem Buchstaben „n“ als Größe angegeben. Ihre Einheit ist [mol].

 

Bezieht man diese Zahl auf eine bestimmte Anzahl an Atomen oder Molekülen, spricht man auch von der Stoffmenge „n“.

 

Berechnung der Teilchenzahl aus der Stoffmenge

Manchmal möchte man, z.B. um sich die atomaren Verhältnisse besser vorzustellen, die Anzahl an Teilchen in einer gewissen Stoffportion berechnen. Das ist mit der Avogadro Zahl nicht schwer.

Möchte man Errechnen, wie viele Teilchen in einem Mol sind, so kann man einfach mit der Avogadrozahl multiplizieren:

 

Beispiel: Bestimme die Anzahl an Teilen in 1,5 mol Zucker:

1,5mol · 6,022·10²³ Teilchen/ mol = 9,033 · 10²³ Teilchen

n · Avogadro Zahl = Anzahl an Teilchen

 

Wie wird die Avogado-Zahl berechnet?

Wie wir wissen, wird die Atommasse in „units“ angegeben. Das hilft, auszurechnen, wie viele Atome in 12g Kohlenstoff enthalten sind.

Gegeben: 1u entspricht 1/12 C-Atom => 1 C-Atom entspricht 12u

Formel: m_a(C) = 12 u

Gesucht: n(C) = 12g/ (12u · 1,6605 · 10^-24g/u) = 1/ 1,6605 • 10^-24g = 6,022 · 10²³

 

Aufgaben:

1. Bestimme die Anzahl an Molekülen, die in 1,8mol Wasserstoff enthalten sind.
2. Ein Chemiker wiegt für einen Schülerversuch 24g Kohlenstoff ab, das entspricht genau 2mol Kohlenstoff. Wie viele Teilchen liegen vor, wenn er dies für 8 Versuchsgruppen macht?
3. Die Zahl 1 Billion scheint für uns sehr groß (=10¹²). Welcher Stoffmenge an Wasser (angegeben in mol) sind nun genau 1 Billion Wassermoleküle?

 

Zusatzinformationen

https://de.wikipedia.org/wiki/Stoffmenge, https://de.wikipedia.org/wiki/Avogadro
https://de.wikipedia.org/wiki/Avogadro-Konstante

 

b) Die Masse von Atomen

Ein Chemiker will natürlich auch wissen, was denn jetzt eigentlich so einzelnes Atom wiegt! Vermutlich weißt Du schon, wie man die Atommasse bestimmt.

Z.B.: ein Cu-Blech wiegt 63,5 g. Eine Messung ergibt, es enthält genau 6,022 10²³ Atome (=1mol)

 

Wie viel wiegt jetzt ein Atom?

m_(Cu-Atom) = 63,5 g : 6,022 10²³ Atome = 1,055 10^-22 g/Atom

 

Diese Zahl ist natürlich absolut unhandlich und viel zu klein, um damit zu rechnen. Keine Waage der Welt, könnte auch nur annähernd solche Massen wiegen (im Labor sind schon drei Nachkommastellen schwer zu wiegen... an 22 Nachkommastellen, wollen wir da lieber nicht denken :-) )

Wir machen es wie der Juwelier³. Wir führen eine eigene Masseneinheit für Atome ein. Die Chemiker haben lange gerätselt, wie sie die neue Einheit nennen können und benannten sie schließlich mit dem englischen Wort für Einheit „unit“.

 

Die Einheit der Atommasse ist „unit“.

Im PSE sind die Massen der Atome in units [u] angegeben.

Während Dalton noch alle Massen im PSE auf das Gas Wasserstoff bezog, bezieht man heute alle Massen der Elemente auf den Kohlenstoff.
Er ist fest und lässt sich leicht wiegen.
Es wurde auf 12u festgesetzt.

 

Wie viel g sind jetzt ein u?

1 u =1/12 der Masse des Kohlenstoffatoms => 1u = 1,6605 · 10^-24g

 

c) Die molare Masse

Sicher hast Du Dich nun schon gefragt, woher Chemiker überhaupt wissen, wie viele Atome z.B. in einem Stück Kohle enthalten sind?⁴ Vielleicht hilft Dir ein Vergleich, um auf die Lösung zu kommen:

Ein Gedankenexperiment hilft uns dabei: Wie kann man bestimmen, wie viele (gleiche) Centmünzen in einer Streichholzschachtel sind, ohne diese zu öffnen oder die Cent einzeln abzuzählen?

Richtig, man kann sie wiegen! Wenn Du die Masse einer Münze kennst, kannst Du leicht die Anzahl in der Streichholzschachtel durch Division bestimmen:

Anzahl Münzen = Masse aller Münzen / Masse einer Münze

 

Zusammenhang zwischen Masse und (Stoff)menge:

Wenn 1 Cent 2g wiegt und die Schachtel mit allen Centmünzen 18g wiegt, dann sind 9 Münzen in der Schachtel.

                               Masse aller Münzen             18g
Anzahl an Münzen = ———————————— = ———— = 9 Centmünzen
                               Masse einer Münze               2g

 

Beziehen wir das nun auf die Massen von Atomen:

Man hat also 12g Kohlenstoff, (z.B. ein kleines Stück Kohle). Man kennt die Masse und möchte nun wissen wie viel Atome es sind.

M = molare Masse [g/mol] (=Umrechnungsfaktor zwischen Masse und Stoffmenge⁵)

m = Masse in g

n = Stoffmenge (also Anzahl an Atomen in mol)

 

                                                        Masse aller Teilchen        m
Anzahl an Teilchen = Stoffmenge n = ——————————— = ——— = n
                                                      Masse eines Teilchens       M

 

=> m = M · n

=> M = m / n

Die molare Masse ist ein Umrechnungsfaktor zwischen der Masse und der Stoffmenge. Ihr Wert kann leicht aus dem PSE abgelesen werden.
Er entspricht dem Wert der Atom- (bzw. Molekül-) Masse. Ihre Einheit ist [g/mol].

 

=> 1 mol Kohlenstoff hat die molare Masse 12,001 g/mol

=> 12,001 g C entsprechen 1mol

 

In der Laborpraxis ist das nun ganz einfach:

Hat man von einem beliebigen Stoff die Stoffmenge 1mol, enthält diese immer 6,022·10²³ Teilchen! Die Atommasse dieser Stoffmenge (von einem mol eines Teilchens) entspricht also immer die Masse dieses Elements in Gramm:

1 mol He-Atome wiegen 4g (M_He = 4g/mol) (1 H-Atom wiegt 1u)

1 mol Sauerstoffgas (O₂) wiegt 2 · 16g (M_O2 = 32g/mol) (1 O-Atom wiegt 16u)

 

Auch für Verbindungen kann die molare Masse angegeben werden. Sie ergibt sich einfach durch

Addieren der Atommassen der Elemente, die in einer Verbindung enthalten sind:

 

z. B.: Bestimme die relative Molekülmasse von Wasser (von Zucker)

M(H₂O) = 2 · 1,008u + 16,00u = 18,016u

=> 1 mol Wasser wiegt 18g (M_H2O = 18g/mol)

 

M(C₆H₁₂O₆) = 6 M(C) + 12 M(H) + 6 M(O)

= (6 · 12 + 12 · 1 + 6 · 16) g/mol

= 180 g/mol

=> 1 mol Zucker (C₆H₁₂O₆) wiegt demzufolge 180g.

 

Zusatzinformationen:

https://de.wikipedia.org/wiki/Molare_Masse
https://de.wikipedia.org/wiki/Mol_Stoffmenge

 

SI-Einheiten (Système International d'unités)

International hat man sich 1960 auf ein einheitliches Einheitensystem für physikalische Größen geeinigt. Einheiten, welche nicht durch andere Einheiten ausgedrückt werden können, nennt man SI-Einheiten (von frz.: Système international d’unités).

Man hat sieben SI-Basiseinheiten festgelegt. Alle anderen Einheiten, können durch SI-Einheiten ausgedrückt werden (so ist die Maßeinheit von Druck, das Pascal, keine SI-Einheit, sondern eine zusammengesetzte Einheit (1 Pa = 1kg/(m·s²)).

 

Größe	Einheitenname	Einheit
Länge	Meter	m
Masse	Kilogramm	kg
Zeit	Sekunde	s
elektrische Stromstärke	Ampère	A
Temperatur	Kelvin	K
Stoffmenge	Mol	mol
Lichtstärke	Candela	cd

Alle internationalen Einheiten werden kleingeschrieben, es sei denn, dass der Name der Einheit von einer Person abgeleitet wurde. Auch „l“ für Liter wird kleingeschrieben! Das große „L“ für Liter wurde ausnahmsweise als alternatives Einheitenzeichen zugelassen, um Verwechslungen des Buchstabens l mit der Ziffer 1 zu vermeiden. Dies findet man aber vor allem im englischen und französischen Sprachraum.

 

Zusatzinformationen:

https://de.wikipedia.org/wiki/Internationales_Einheitensystem

 

Aufgaben zum Thema molare Masse

 

1. Bestimme die molare Masse von: C, H, O, H₂O, HCl, H₃PO₄, C₈H₁₄

2. Du kennst nun die Anzahl an Atomen in einem 12,00g schweren Kohlenstoffstückchen, aber wie viele Atome sind in einem doppelt so schweren Kohlestückchen enthalten? Notiere die Zahl ;-)

3. Bestimme die Stoffmenge und die Anzahl an Molekülen in 100,00g Zucker (C₆H₁₂O₆).

4. Bestimme die Stoffmenge von 1,000kg Eisen.

5. 1 Liter Schwefelsäure enthält 18,00 mol Schwefelsäuremoleküle. Bestimme die Masse.

6. 10,00g Magnesium reagieren mit Salzsäure zu einem Gas und einem Salz.
   a) Stelle die Reaktionsgleichung auf
   b) Bestimme die Stoffmenge an Magnesium und die Anzahl an Atomen
   c) Bestimme beide Werte auch für das Salz.

   d) Bestimme die Masse des Salzes.

7. Welche Stoffmenge ist in einer mit Wasser gefüllten Badewanne (200l) enthalten?
   (Dichte von Wasser: ρ = 1,00g/ml)

8. Befinden sich mehr Atome in 1,000kg Gold oder in 150,000g Aluminium?

9. Eine Stoffportion hat eine Masse von 1,520g. Die Stoffmenge beträgt 0,033mol. Wie lautet die molare Masse des unbekannten Reinstoffs.

10. Es ist gewünscht für ein Experiment eine 0,100molare Silbernitratlösung darzustellen. Wie muss man vorgehen? (Tipp: molar bedeutet mol/l)

11. Bei der Verbrennung von 1,00l Benzin (entspricht einer Autofahrt von ca. 10-14km) entsteht 2,32kg CO₂. Das entspricht einem Volumen von ca. 1000l! Berechne die Anzahl an entstehenden CO₂-Molekülen. Das entspricht einem Volumen von ca. 1000l! Berechne die Anzahl an entstehenden CO₂-Molekülen.

Lösungen

8)

m= 1,52 g.

M= ?

n= 0,033 mol

 

         m        1,52g
M = —— = ————— = 46 g/mol Die molare Masse der Stoffportion ist 46 g/mol.
         n      0,033mol

 

9) Ziel: Herstellung einer Lösung mit 0,1mol/l Silbernitratlösung

M_Silbernitrat = 169,87 g/mol

n_Silbernitrat = 0,1mol

m_Silbernitrat = ?

 

m = M · n => m = 169,87 g/mol · 0,1mol = 16,987g Silbernitrat

16,987g Silbernitrat müssen also abgewogen werden, um dann im Messzylinder mit destilliertem Wasser auf die 1Liter-Marke gefüllt werden.

 

Die Dichte

Mit dem Begriff der Dichte haben wir uns schon ganz am Anfang des Chemiekurses beschäftigt. Hier noch einmal das Wichtigste und einige Übungen zur Berechnung.

Die Problemfrage lautet: Wie kann man zwei Körper unterschiedlicher Form hinsichtlich ihres Gewichtes vergleichen?

Eigentlich gar nicht! Ein großer Ordner aus Papier und Pappe wird schwerer sein als ein Eisennagel. Aber ist Papier damit schwerer als Eisen?

Zum exakten Vergleich, muss man immer das Volumen mit in Betracht ziehen, sonst könnte man meinen, Papier sei schwerer als Eisen.

 

Bestimmung der Dichte:

Ein Körper (z.B. ein Aluminiumstückchen) wird gewogen und sein Volumen bestimmt (z.B. durch Ansteigen von Flüssigkeit in einem Standzylinder.).

Durch Wiegen und Verdrängung von Wasser im Messzylinder kann immer das Volumen eines Körpers und somit seine Dichte leicht bestimmt werden.

Es gilt: 1l entspricht 1000cm³.

Die Dichte (Formelzeichen: ρ (griechisch: rho)), ist das Verhältnis der Masse (m) eines Körpers zu seinem Volumen (V). Die Dichte ist eine Stoffeigenschaft.

m
ρ = ————
V

Die Einheit der Dichte ist kg/m³.

Oft ist die Dichte jedoch in g/cm³ angegeben.

 

Manchmal wird die Dichte auch als spezifisches Gewicht ausgedrückt⁶.

 

Einige Dichten bei Normaldruck in der vorgeschriebenen SI-Einheit

 

Stoff	Dichte in g/cm3
Platin	21,45
Gold	19,32
Wolfram	19,25
Uran	18,05
Quecksilber	13,59
Blei	11,34
Silber	10,49
Wismut	9,8
Kupfer	8,95
Nickel	8,9
Konstantan	8,8
Kadmium	8,6
Messing	8,5
Bronze	8
Eisen	7,86
Stahl	7,8
Zinn	7,28
Zink	7,13
Chrom	6,92
Titan	4,5
Kohlenstoff	3,51
Aluminium	2,7
Glas	2
Silizium	2,33
Schwefel	2,07
Beton	2
Phosphor	1,82
Beryllium	1,8
Magnesium	1,73
Sand	1,65 (je nach Typ bis 2,1)
Meerwasser	1,03
Wasser (bei 3,98 °C)	1
Eis (bei 0 °C)	0,92
Holz	0,90 (je nach Typ bis 1,1)
Schmieröl	0,9
Alkohol/ Spiritus	0,79
Benzin	0,68
Kalium	0,68
Schaumstoff	0,035
Kohlenstoffdioxid	1,250 ·10-3
Luft	1,290 ·10-3

 

Umfangreiche Tabellen unter:

• https://de.wikipedia.org/wiki/Dichte
• https://de.wikibooks.org/wiki/Tabellensammlung_Chemie/_Dichte_fester_Stoffe
• https://de.wikibooks.org/wiki/Tabellensammlung_Chemie/_Dichte_flüssiger_Stoffe
• https://de.wikibooks.org/wiki/Tabellensammlung_Chemie/_Dichte_gasförmiger_Stoffe

 

Aufgaben zum Thema „Dichte“

1. Kennst du das Märchen „Hans im Glück“, in dem Hans einen Goldklumpen geschenkt bekommen hat, der so groß wie sein Kopf ist (Volumen etwa 4 dm³)? Wie schwer war der Goldklumpen eigentlich, den Hans einfach in ein Tuch wickelte und dann über die Schulter warf, um zu gehen?
2. Du vergleichst je 1kg Benzin, Öl und Wasser in Messbecher eingefüllt. Welche Flüssigkeitsmenge ist jeweils enthalten?
3. Für eine Sporthalle soll ein Fundament mit der Fläche 20m · 60m mit der Dicke von 80cm mit Beton ausgegossen werden. Wie groß ist die Masse des erforderlichen Betons?
   (Dichte Beton = 2,0 g/cm³)
4. Kann man 9kg Quecksilber in eine 0,7l-Wasserflasche Flasche füllen?
5. Eine Sprudelflasche ist mit 1l Wasser gefüllt und hat die Masse 1,40 kg. Welche Masse hat das Glas der Flasche?
6. Ein Wassertransporter der Feuerwehr hat ein Fassungsvermögen von 10 000,00 l. Das Fahrzeug hat eine Masse von 4,5t.
   (1l Wasser = 1 000 cm³). Welches Gewicht hat das mit Wasser beladene Fahrzeug?
7. Ein Transporter ist auf dem Weg zur Baustelle 30,00 cm hoch mit Betonplatten belegt. Wie hoch könnte man ihn bei gleichem Gewicht mit Schaumstoff beladen?
8. a) Bestimme die Stoffmenge an Chlorwasserstoff, welche sich in einem Liter einer 37%igen Salzsäure befindet.⁷ (Dichte von 37%iger Salzsäure = 1,19 g/cm³)
   b) Im Labor geht man oft den umgekehrten Weg. Aus einer Flasche mit konzentrierter (also 37%iger) Salzsäure soll eine 1molare (also 1 mol / l) Lösung hergestellt werden. Wie muss man vorgehen?

 

Lösungen

1.

V = 4dm³ = 4·10³ cm³

ρ = 13,3 g/cm³

m = ?

 

          m
ρ = ——— => m = ρ·V => 4·10³ cm³ · 13,3 g/cm³ = 77,2kg (bissel schwer, für die Schulter ;-) )
         V

 

2.

ρ_Benzin = 0,7 g/ cm³

ρ_Öl = 0,9 g/ cm³

ρ_Wasser = 1 g/ cm³

Vergleicht man nun jeweils 1 kg jeder Substanz, so benötigt die Substanz mit der geringsten Dichte das meiste Volumen.

=> V_Benzin = 0,7l

V_Öl = 0,9l

V_Wasser = 1l

 

3.

V = 960 m³
ρ = 2,0 g/cm³ entspricht 2000kg/m³

m = ?

m = ρ · V = 2000 kg/m³ · 960 m³ = 1920000kg

Es werden 1920t Beton benötigt... Hut ab, das ist ein echt schwerer Boden...

 

4.

ρ_Hg = 13,6 g/ cm³

m_Hg = 9000g

V = ?

 

V = m/ρ = 9000g/ 13,6 g/ cm³ = 661 cm³

=> Ja, man kann es in eine 0,7l Flasche einfüllen.

 

5.

V_H2O = 1l

m_Flasche = 1,4kg

V = ?

ρ_Wasser = 1g/ cm³

ρ_Glas = 2,5 g/ cm³

 

=> Masse des Wassers = m_Wasser = ρ · V

= 1g/ cm3 · 1000cm³ => 1l Wasser hat eine Masse von 1000g => Die leere Flasche wiegt 400g.

 

8a) Zuerst berechnet man die Konzentration einer 37%ige Salzsäure:

M_HCl = 36,46 g/mol
Dichte_HCl : 1,19 g/cm³

Aus der Prozentangabe weiß man, dass in 1000g 37%iger Salzsäure also 370g HCl-Gas gelöst sind. Aber wie viel ist das pro Liter?

 

          m
ρ = ——— => ρ · V = m => m = 1,19g/cm³ · 1000cm³ = 1190g
          V

 

Ein Liter 37%ige Salzsäure wiegt also 1190g! 37% davon sind also 1190g · 0,37 = 440,3 g

Diesen Wert können wir nun in die Gleichung zur molaren Masse einsetzen:

 

n_HCl = ?

m_HCl = 440,3g

M_HCl = 36,46 g/mol

 

n = m / M => n = 440,3 g : 36,46 g/mol = 12,07 mol (gilt für einen Liter!)

37%ige Salzsäure besitzt eine Molkonzentration von ca. 12 mol/l.

 

8b) Aus dieser 37%iger Salzsäure soll eine 1molare Lösung hergestellt werden. Aus a) wissen wir, das ein Liter 12mol enthält. Welches Volumen braucht man also für 1 mol?

Rrrrichtig: 1/12 l = 0,0833 Liter :-)

Damit man ein Liter dieser verdünnten Lösung bekommt, muss man 0,0833 Liter 37%ige Salzsäure mit Wasser auf 1 Liter Lösung auffüllen!

 

Avogadro’s Gasgesetz und seine Anwendung

Der italienische Graf Amedeo Avogadro (1776-1856) war zugleich Physiker und Chemiker und führte Untersuchungen mit Gasen durch. Ihn beschäftigte vor allem die Frage nach dem Volumen von Gasen. Durch seine Forschungen gelangte er schließlich zu einem erstaunlichen Gesetz:

Satz des AVOGADRO:

Verschiedene Gase haben bei gleichem Druck und gleicher Temperatur das gleiche Volumen
und enthalten somit die gleiche Anzahl an Teilchen (Molekülen oder Atomen).

 

Mit diesem Wissen ausgestattet, stellte er weitere Forschungen an und bestimmte nun die (relative) Atommasse von gasförmigen Elementen. Dies hatte wegen der schlechten Verfügbarkeit und der schwierigen Handhabbarkeit vor ihm noch niemand versucht.

Er definierte die so genannte Avogadro-Konstante⁸, nach der in einem Mol, die Anzahl von genau 6,0221367 · 10²³ Molekülen oder Atomen angibt. Heute spricht man auch von „Stoffmenge“.

Avogadros Forschungen waren zwar derart grundlegend und wichtig, dennoch waren sie zu seiner Zeit sehr umstritten. Heute weiß man, das ein Mol einer Substanz stets dieselbe Anzahl von Teilchen hat, unabhängig davon, ob sie fest, flüssig oder gasförmig vorliegt.

(Zusatzinformationen unter https://de.wikipedia.org/wiki/Avogadro)

 

Konsequenzen und Anwendung des Avogadro’s Gasgesetzes: Die Chlorknallgas-Reaktion

1l Wasserstoffgas [H₂] enthält genau so viele Wasserstoffmoleküle, wie 1l Chlorgas Cl₂ - Moleküle

H₂ + Cl₂ ---> 2 HCl + E

d.h.: 1l = x mol H₂ + 1l = x mol Cl₂ ---> 2 ·1l = 2 · x mol HCl + E

 

Konsequenzen: Das bedeutet, dass das Massenverhältnis m(H) : m(Cl) sich durch einfaches Wägen der beiden Gasportionen und Dividieren der erhaltenen Ergebnisse durch den kleineren Massenwert ermitteln lässt:

m(H)/m(Cl) = 1/35

=> Ein Chloratom ist also 35mal schwerer, als ein Wasserstoffatom. So kann man die Atommassen relativ zueinander bestimmen:

=> M_(H) = 1u M_(Cl) = 35u => 1u = 1,661·10^-24g

 

Auf diesem Wege lassen sich die relativen Atommassen aller verdampfbaren Elemente ermitteln.

Anwendung: Mit „units“ zu rechnen ist im Alltag allerdings nicht immer praktikabel, da nur wenige Menschen dies verstehen. Die gebräuchliche und auch im Laboralltag angewendete Masseneinheit ist nicht das „unit“, sondern das „Gramm“. Ersetzt man also bei den Atommassenangaben die Einheit „unit“ durch „Gramm“, so erhält man von jedem Element eine genaue Stoffmenge (n), die der Chemiker als 1mol dieses Elements bezeich­net. Die dazugehörige Masse wird als Molare Masse (M) bezeichnet und besitzt die Einheit g/mol.

 

M_(H) = 1,0 g/mol M_(Cl) = 35,5 g/mol M_(HCl) = 36,5 g/mol

=> 1mol Chlorwasserstoffgas hat ein Gewicht von 36,5g

 

Molares Volumen (V_M)

Nun müssen nur noch die Regeln für Gase aufgestellt werden, dann hast Du bereits alles Wichtige gelernt. Bei Gasen gab es ja eine Besonderheit, die Avogadro entdeckt hatte.

Stell Dir vor: Ein Gas nimmt bei 0°C und 1013 hPa ein Volumen von 1,4 l ein. Könnte man die vorhandene Stoffmenge bestimmen, obwohl man nicht weiß welches Gas vorliegt? (Vergleich: zwei gefüllte Luftballons).

 

Die Frage, die sich stellt: Gibt es einen Umrechnungsfaktor zwischen Volumen und Stoffmenge?

Bedenke:

Wenn gleiche Volumen verschiedener Gase unter gleichem Druck und gleicher Temperatur immer die gleiche Anzahl von Teilchen enthalten (Gesetz des Avogadro), so besitzt doch die Stoffmenge 1 mol aller Gase unter gleichen Bedingungen auch immer das gleiche Volumen, oder?

 

=> Bei gleichem Volumen ist unabhängig vom Gas immer die gleiche Stoffmenge vorhanden.

 

Nur welche Stoffmenge ist dies?

es gilt: V (eines Gases) ist proportional zu n

=> V = n · V_M

V_M = molares Volumen [l/mol]

=> V = n · 22,4 l/ mol

=> n = 10l / 22,4 l/ mol = 0,45 mol

 

Das molare Volumen ist ein Umrechnungsfaktor zwischen Stoffmenge und Volumen. Für Gase⁹ hat es bei Normalbedingungen (0°C und 1013 hPa) immer den Wert 22,4 l/mol.

=> Das Molare Volumen V_M ist für Gase eine unveränderbare Konstante: V_M = 22,4 l/mol

=> 22,4 l eines beliebigen Gases enthalten 1mol Teilchen.

 

 

Beachte: der genaue Wert gilt nach Avogadro nur für Normalbedingungen:

Molare Volumen bei Normalbedingungen (0°C (=273K), 1013,25 hPa) = 22,413996 l/mol

 

Im Labor sind allerdings höhere Temperaturen üblich, deshalb rechnet man hier oft mit den angepassten Standardbedingungen:

Molare Volumen bei Standardbedingungen (25°C (=298K), 1013,25 hPa) = 24,4640424 l/mol

 

Beispielaufgabe:

Welches Volumen nehmen 10mol Wasserstoff (bzw. 10l Erdgas?) ein?
V = V_M ^. n = 22,4 l/mol => 10mol = 224 l (das gilt für alle Gase!)

 

Zusatzinformationen:

• https://de.wikipedia.org/wiki/Molares_Volumen
• https://de.wikipedia.org/wiki/Normalbedingungen
• https://de.wikipedia.org/wiki/Standardbedingungen

Aufgaben zum Thema „molares Volumen“

Für alle Rechnung mit Gasen gelten, sofern nicht anders angegeben, Normalbedingungen

1. a) Wie viel Teilchen befinden sich in einem mit einem Atemzug leicht aufgeblasenen Luftballon (pro Atemzug kann man ca. 500,00ml ein- und ausatmen => Pro Minute ca. 8l).
   b) Macht es dabei einen Unterschied, ob man mit Sauerstoff, Luft oder Stickstoff rechnet?
   c) Wie viele Teilchen sind das Pro Tag?
2. Wie viel Liter Wasserstoffgas werden benötigt, um 10mol HCl zu bilden? Verwende als Reaktionspartner Chlorgas.
3. Ein Luftballon enthält 5,00l Helium.
   a) Berechne die Stoffmenge sowie die Anzahl der tatsächlich enthaltenen Atome
   b) Wie groß ist die Masse, wenn der Luftballon selbst 11,00g wiegt. Warum steigt er dennoch auf?
4. Magnesium wird mit einer schwachen Salzsäure vermischt. Es entsteht ein Gas.
   a) Stelle die Reaktionsgleichung auf und bestimme die Formel und den Namen des Gases
   b) Welches Gasvolumen entsteht bei Verwendung von 10,0g Magnesium?
5. 2,24l Wasserstoff werden entzündet.
   a) Welches Sauerstoffvolumen ist notwendig, damit die Reaktion vollständig abläuft
   b) Stelle die Reaktionsgleichung auf und benenne die Reaktion
   c) Wie viele Moleküle des Produkts entstehen?
   d) Das Produkt entsteht als Gas. Welches Volumen wird es haben.
   e) Warum ist das Ergebnis aus d) sehr ungenau?
6. Stelle das Salz Zink(II)-chlorid her. Verwende dazu die passende Säure und ein Element.
   a) Stelle die Reaktionsgleichung auf
   b) Wie groß ist die Masse des Elementes, die notwendig ist, um mindestens 4l des zweiten gasförmigen Produkts zu bilden?
7. Ein unbekanntes Gas hat laut einem Experiment die Dichte von ρ=1,96 g/cm³. Wie lautet die molare Masse des unbekannten Reinstoffes? Wie heißt das Gas?

 

Spickzettel: Übersicht zum Rechnen mit chemischen Größen

Symbole und Einheiten

 

Größe	Symbol	Einheit
Stoffmenge	n	mol
Masse	m	g
Atommasse	m	u
Molare Masse	M	g/mol
Volumen	V	l
Molares Volumen	Vm	l/mol
Avogadrozahl	NA	mol-1
Stoffmengenkonzentration	c	mol/l

 

Zusammenhänge

Stoffmenge (n) und Molare Masse (M):

n (mol) = m / M

=> m = n · M

=> n = m/ M

 

Stoffmenge (n) und Molarem Volumen (VM):

V_M = V/ n

=> n = V / V_M

=> V = V_M· n

 

Stoffmenge (n) und Konzentration (c):

c = n / V(Lösung)

 

Dichte:

δ = m/ V

=> δ · V = m

 

molare Masse und molares Volumen:

m/M = V/V_M

bzw: n · M = δ · V

 

Gruppenarbeit: Aufgaben mit abgestuften Niveau

Aufgaben mit mittlerem Niveau:

1. Wie groß ist die molare Masse von: H, O, H₂O, HCl, H₃PO₄?

2. Wie viele Atome sind in 6g Zucker enthalten?

3. 5g Calcium reagieren mit Salzsäure zu einem Gas und einem Salz.
a) Stelle die Reaktionsgleichung auf.
b) Bestimme die Stoffmenge an Calcium.
c) Bestimme beide Werte auch für das Salz.

4. Eine Stoffportion hat eine Masse von 1,52g. Die Stoffmenge beträgt 0,033mol. Wie lautet die molare Masse des unbekannten Reinstoffes? Um welchen Stoff handelt es sich?

 

Hilfen für Aufgaben mit mittlerem Niveau:

1. Die molare Masse kann im PSE abgelesen werden.

2. Die Anzahl an Atomen kann über die Stoffmenge bestimmt werden. Errechne zuerst diese Stoffmenge und wandle dann mit der Avogadrozahl um.

3. Das Salz ist Calciumchlorid. Wie bestimmt man seine Formel?

4. Schau mal im PSE, ob Du die molare Masse zuordnen kannst... ;-)

------------------------------------------------------------------------------------------------------------------------------------------

 

Aufgaben mit hohem Niveau:

1. Wie groß ist die molare Masse von: H, O₂, H₂O, HNO₃, H₃PO₄, C₈H_14, C₆H₁₂O₆?

2. Wie viele Atome sind in 6g Zucker enthalten? Wie viele in 60g?

3. Überprüfe: 1000000 Millionen Moleküle Pb sind schwerer als 10 000 000 Moleküle Aluminium

4. 5g Calcium reagieren mit Salzsäure und bilden dabei zwei Produkte, von denen eines ein Salz ist.
a) Stelle die Reaktionsgleichung auf und bestimme die Stoffmenge an Calcium und die Anzahl an Atomen
b) Bestimme beide Werte auch für das Salz

5. Eine Stoffportion hat eine Masse von 1,52g. Die Stoffmenge beträgt 0,033mol. Bestimme über die molare Masse den Namen des Stoffes.

 

Hilfen für Aufgaben mit hohem Niveau:

1. Die molare Masse kann im PSE abgelesen werden.

2. Die Anzahl an Atomen kann man aus dem Produkt aus molarer Masse und Avogadrozahl bestimmt werden.

3. Berechne die beiden Massen unabhängig voneinander.

4. Ein Produkt ist Wasserstoff.

5. Siehe PSE ;-)

------------------------------------------------------------------------------------------------------------------------------------------

 

Aufgaben mit Expertenniveau:

1. 5,00g Calcium reagieren mit Salzsäure und bilden dabei zwei Produkte, von denen eines ein Salz ist.
a) Stelle die Reaktionsgleichung auf und bestimme die Stoffmenge an Calcium und die Anzahl an Atomen.
b) Bestimme beide Werte auch für das Salz.

2. 1,000kg Gold und 150,000g Aluminium werden verglichen. Treffe Aussagen hinsichtlich molarer Masse, der Stoffmenge (in welcher Stoffportion befinden sich mehr Atome?) und der Teilchenanzahl.

3. Eine Stoffportion hat eine Masse von 1,52g. Die Stoffmenge beträgt 0,033mol. Bestimme den Namen des Stoffes.

4. Es ist gewünscht für ein Experiment eine 0,1molare Silbernitratlösung darzustellen. Wie muss man vorgehen? (Tipp: molar bedeutet mol/l)

5. Bei der Verbrennung von 1,00l Benzin (entspricht einer Autofahrt von ca. 10-14km) entsteht 2,32kg CO₂. Das entspricht einem Volumen von ca. 1000l! Wie viele Moleküle CO₂ entstehen?

 

Hilfen für Aufgaben mit Expertenniveau:

1. Erdalkalimetalle bilden mit Säureresten oft Salze

2. Berechne zuerst soweit noch notwendig n, m, M

3. Berechne die molare Masse und vergleiche mit dem PSE

4. Bedenke, 1l Wasser entspricht 1000ml, diese wiegen 1000g

 

Bestimmung der Größe von Ölsäuremolekülen

Ölsäure ist eine Substanz, die sich auf Wasser solange fein verteilt, bis eine Schicht entsteht, bei der ein Molekül neben einem anderen liegt und keine Stapel mehr vorliegen. Die Höhe dieser Schicht ist also genau so hoch, wie der Durchmesser eines Moleküls.

Um diesen zu bestimmen, wird Ölsäure 1/ 2000 in Benzin verdünnt .

V: 0,1cm³ Ölsäure wird in 200 cm³ Benzin verdünnt. Davon wird 1 cm³ abgefüllt und durch Zählen der Tropfen einer Pipette bestimmt, wie viel Tropfen dies entspricht (ca. 72):

1 Tropfen entspricht dann ca. 0,7 · 10^-5 cm³ Ölsäure

Gemessen wird dann die Fläche, die ein solcher Tropfen auf einer Wasseroberfläche hat

(mit Korkspänen und Millimeterpapier)

Berechnung: V= F·h

 

 

Welche Informationen liefert eine Reaktionsgleichung?

Wenn wir jetzt alles aus diesem Kapitel zusammenfassen, dann lässt sich nun viel mehr aus einer Reaktionsgleichung ablesen, als Du vermutlich bis jetzt vermutet hast!

Eine kleine Warnung: Auch wenn das beim ersten Lesen jetzt recht einfach und trivial wirkt, so sind die dahinter liegenden Aussagen es nicht! Denke einmal Zeile für Zeile über diese Aussagen nach!

 

Reaktions- gleichung:		O2	+	2 H2	--->	2 H2O
Qualitative Aussage:		Sauerstoff	+	Wasserstoff	--->	Wasser
Quantitative Aussagen:
	Mengen:	1 Molekül O2	+	2 Moleküle H2		2 Moleküle H2O
		1 mol O2	+	2 mol H2	--->	2 mol H2O
	Masse:	1 . 32 u	+	2 . 2 u	--->	2 . 18 u
		1 . 32 g	+	2 . 2 g	--->	2 . 18 g
	Volumen (bei Gasen):	1 . 22,4 l	+	2 . 22,4 l	--->	2 . 22,4 l

 

Hinweis: Die beteiligte Energie der Reaktion kann zusätzlich noch angegeben werden. Die Angabe dieser Energie (auch Reaktionsenthalpie genannt) ermöglicht Aussagen und Berechnungen zu exakten Energiebeteiligung:

ΔE_{(Knallgasreaktion)} = - 286 kJ => exotherme Reaktion

 

Aufgaben:

1. Nenne Aussagen der folgenden Reaktionsgleichungen.

N₂ + 3 H₂ + E ---> 2 NH₃

CH₄ + 3 O₂ ---> CO₂ + 2 H₂O + E

4Fe + 3O₂ ---> 2Fe₂O₃ + E

2. Bei der Verbrennung von 10g Schwefel entsteht der Feststoff SO₃.
a) Stelle die Reaktionsgleichung auf.
b) Wie viel Produkt entsteht aus 10g Schwefel?
c) Wie viel Sauerstoff wurde bei dieser Verbrennung benötigt?

 

Die Reaktion von Magnesium mit Salzsäure

V: In einem Reagenzglas mit seitlichem Auslassrohr bzw. einem mit durchbohrtem Stopfen werden 0,100g Mg gefüllt und mit ca. 5cam HCl überschichtet. Das Reagenzglas wird sofort verschlossen und das Gas (vorsichtig) mit einem Kolbenprober aufgefangen. Die Gasmenge wird bestimmt und anschließend berechnet, ob man das komplette Gas aufgefangen hat.

 

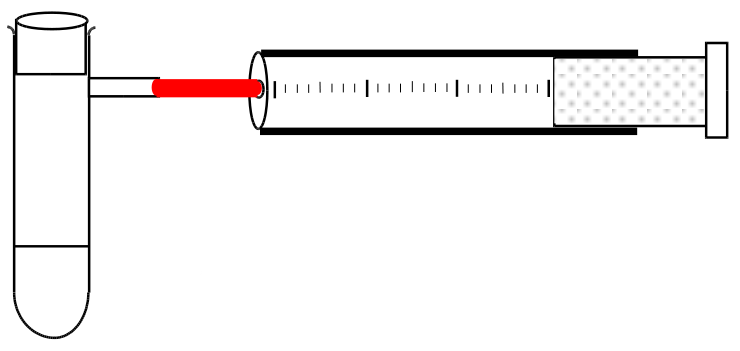
B: Das Gemisch wird warm, ein Gas bildet sich, es entstehen ...ml Gas

S: Magnesium reagiert unter Wärmebildung mit Salzsäure. Die entstehende Wärme erwärmt die Flüssigkeit.

Magnesium + Salzsäure ---> Magnesiumchlorid + Wasserstoff + E

Mg + 2HCl ---> MgCl₂ + H₂ + E

 

Berechnung: Welches Volumen müsste theoretisch entstehen?

gesucht: V(H₂) = ?

gegeben: Vm = 22,4 l/mol => die Berechnung mit V = Vm · n ist nicht möglich, da n nicht gegeben ist.

Aus den Aussagen der Reaktionsgleichung folgt aber, dass die Stoffmengen der Ausgangsstoffe und die Stoffmengen der Produkte miteinander im angegebenen Verhältnis stehen.

Das heißt:

1 mol Mg + 2 mol HCl ---> 1 mol MgCl₂ + 1 mol H₂

bzw. n mol Mg + 2n mol HCl ---> n mol MgCl₂ + n mol H₂

 

Mit anderen Worten, wenn man die Stoffmenge von Mg kennt, dann weiß man auch die Stoffmenge des entstehenden H₂.

m(Mg) = 0,100g

M(Mg) = 24,305g/mol

n(Mg) = gesucht = n(H₂) n= m/M

        0,100g
=> ——————— = 0,0041mol Mg bzw. H₂
      24,305g/mol

 

Dieser Wert wird nun in die erste Gleichung eingesetzt und man erhält:

V = Vm · n = 22,413mol/l · 0,0041mol = 0,0922l (= 92,2ml) H₂ entstehen tatsächlich

 

Die Konzentration „c“

Die Anzahl an Teilen in einer Lösung ist für Chemiker oft sehr interessant. Diese haben wir mithilfe der molaren Masse gut berechnen können. Die Anzahl an Teilchen wird in mol angegeben.

Nur ist der Vergleich zweier Lösungen schwierig, wenn man zwei Lösungen mit verschiedenen Volumina hat. Wir brauchen also eine neue Größe, die diesen Vergleich erlaubt.

Eine Problemfrage verdeutlicht dies:

Ist eine Säure A mit 1 mol Säureteilchen in 100ml Wasser stärker oder schwächer, als die gleiche Säure B mit 0,5 mol Säureteilchen in 75ml Wasser?

Um eine korrekte und vergleichbare Aussage zu treffen, sollte das Volumen keine Rolle spielen. Man kann also durch das Volumen teilen, sodass das Ergebnis vom Volumen unabhängig ist. Der entstehende Wert wird Konzentration genannt. Sein Symbol ist c und die Maßeinheit [mol/l]

 

n
c = ------ 
V

Umgerechnet:

n = c · V

V= n/c

 

Zum Vergleich: Wenn ein Auto mit 100km/h fährt, dann interessiert uns die tatsächliche Zeit auch nicht, deswegen teilt man durch die Zeit: V = s/t (km pro Stunde). Gleiches macht man bei der Konzentration.

 

Zur oben gestellten Aufgabe:

Lösung A:

V = 100ml = 0,1l

n = 1mol

=> c = n/V = 1mol / 0,1l = 10 mol/l (also eine sehr starke, hochkonzentrierte Säure!

 

Lösung B:

V = 75ml = 0,075l

n = 0,5mol

=> c = n/V = 0,5mol / 0,075l = 6,66 mol/l (auch eine starke Säure, aber schwächer als Säure A!)

 

Lösung A ist die stärkere Säure, da sie mehr Säureteilchen pro Volumen enthält!

 

Zusatzinformationen:

Beachte, wie immer beim chemischen Rechnen Groß- und Kleinschreibung. Die Konzentration und die Stoffmenge haben Kleinbuchstaben (c, n). Das Volumen einen Großbuchstaben (V).

 

Übungen des stöchiometrischen Rechnens I

Aufgaben zur „molaren Masse“:

1. Ein Taucher hat einen Eisengürtel von 2,000kg.
   a) Welche Stoffmenge ist in 2,000kg Eisen enthalten?
   b) Was wiegt die gleiche Stoffmenge, wenn der Gürtel aus Blei wäre?
2. Ein Stecknadelkopf enthält 0,0018mol Eisenatome. Wie schwer ist er?
3. 1,99 mol eines unbekkannten Gases wiegen 32,03g. Bestimme die molare Masse und den Namen des Gases.
4. 20,00g Magnesium reagieren mit Salzsäure. Bestimme mithilfe der Reaktionsgleichung die Produkte und bestimme dann die Stoffmenge und die Masse des entstehenden Gases.
5. Bestimme die Masse von 2,81690mol Chlorgas. Bestimme die Stoffmenge der gleichen Masse Helium.
6. Die Sonne besteht zu ¾ aus Wasserstoff und ¼ aus Helium. Ihre Masse beträgt 1,98 · 10³³g.
   Bestimme die vorhandene Stoffmenge der beiden Gase.

 

 

Aufgaben zum „molaren Volumen“:

(Für alle Berechnungen gelten Normalbedingungen)

1. Ein Liter Benzin setzt 55,00mol Kohlenstoffdioxid frei (ca. 10km Autofahrt!).
   Welcher Masse CO₂ entspricht das und wie viel Litern Gas entspricht das?
2. a) In einer Neonröhre befinden sich 200,00ml Neon. Wie groß ist die Stoffmenge?
   b) Wenn das Gas beim Öffnen einer Neonröhre entweicht, dringt Luft ein. Wie viel mol Luft sind eingedrungen?

 

Aufgaben zur „molaren Masse und dem „molaren Volumen“:

1. a) Welche Masse haben 2,00mol Sauerstoff?
   b) Welche Masse haben 10,00l Sauerstoff?
   c) Wie viel Moleküle sind in 10,00l Sauerstoff enthalten?
   d) Wie viel Moleküle sind in 10,00g Sauerstoff enthalten und welches Volumen nehmen sie ein?
2. Welche Stoffmenge ist in 100,00g Kohlenstoffdioxid enthalten?
3. 0,125 g eines Gases nehmen ein Volumen von 1,400 l ein.
   a) Wie groß ist die molare Masse?
   b) Um welches Gas handelt es sich?
4. 2,456 g eines Gases nehmen ein Volumen von 2,000l ein. Um welches Gas handelt es sich?

 

Aufgaben zur „mol. Masse, dem „mol. Volumen“ und der Dichte:

1. Erstelle eine Formel in der die Dichte, das Volumen, und die molare
   Masse auftauchen.
2. Welche Dichte hat Kohlenstoffdioxid bei Normalbedingungen?
3. Ein Wassertropfen an einem Blatt wird gewogen. Seine Masse beträgt genau 1,8mg.
   a) Wie viel Wassermoleküle sind enthalten?
   b) Mit einer besonderen Technik werden alle Wassermoleküle markiert. Der Tropfen wird dann in den Starnberger See geschüttet (der See hat ca. 2,70 Billionen Liter Inhalt). Der See wird gut vermischt und man entnimmt an einer beliebigen Stelle genau einen Milliliter. Wie viele der ursprüngliche markierte Moleküle würde man dann in einem Milliliter des Starnberger Sees wieder finden? ;-)

Aufgaben zur „Konzentration“:

1. Welches Wasservolumen ist notwendig, damit 0,50mol Zucker eine
   Konzentration von 10mol/l haben?
2. 1 Liter hochkonzentrierte Salzsäure (12mol) soll mit Wasser so verdünnt werden, dass eine verdünnte Salzsäure mit einer Konzentration von 0,5 mol/l entsteht. Bestimme das notwendige Volumen an Wasser.
3. Eine Teetasse mit 0,15l Fassungsvermögen enthält genau 80ml Tee.
   Es werden zwei Zuckerwürfel mit jeweils 3g Traubenzucker zugefügt.
   Die Formel für Traubenzucker ist C₆H₁₂O₆.
   a) Bestimme die Stoffmenge des Zuckers
   b) Bestimme die Konzentration an Zucker im Tee
4. Es sollen 100ml isotonische Kochsalzlösung mit einer Konzentration von
5. 120mmol/l (=0,10mol/l) zum Aufbewahren von Kontaktlinsen hergestellt
6. werden. Berechne die notwendige Masse.
7. Konzentrierte Schwefelsäure hat eine Konzentration von ca. 18,00 mol/l
8. a) Welche Stoffmenge befindet sich in 50,00ml konzentrierter H₂SO₄?
   b) Nun werden diese 50,00ml auf einen Liter mit Wasser aufgefüllt. Hat sich
   die Stoffmenge geändert? Bestimme auch die neue Konzentration.
9. Für diese Aufgabe musst Du eine neue Formel „erfinden“:
   Damit Fische im Aquarium atmen können muss Sauerstoff gelöst sein.
   Bei 20°C sind 0,0091g O₂ in einem Liter Wasser gelöst. Bestimme die Konzentration.
   
   

Zusatzübungen des stöchiometrischen Rechnens

1. In einem Luftballon befinden sich 2 Liter Helium. Wie viele Atome sind enthalten? Wie viele Sauerstoffatome befinden sich in einem Luftballon mit dem gleichen Volumen, wenn 100% Sauerstoff enthalten sind? Wie viele wenn Luft enthalten ist?
2. Wenn Zink mit Salzsäure reagiert, entsteht ein brennbares Gas. Stelle die Reaktionsgleichung auf und berechne die notwendige Zinkmasse, damit mindestens 500ml Gas entstehen.
3. In einer Flasche Chianti sind 0,75l Rotwein enthalten. Auf dem Etikett steht unten die Angabe, das 12,00 Volumenprozent Alkohol enthalten sind. Berechne das Volumen an Alkohol in Litern? Warum ist die Angabe nicht in Massenprozent?
4. Ein normaler Atemzug enthält ca. 0,50l Luft.
   a) Wie viele Sauerstoffmoleküle werden pro Atemzug eingeatmet? (Bedenke: Luft ≠ Sauerstoff).
   b) Durch die Zellatmung reagiert dieser Sauerstoff mit vorher gegessenem Traubenzucker (C₆H₁₂O₆). Stelle die Reaktionsgleichung auf und berechne die Traubenzuckermasse, die mit einem Atemzug umgesetzt wird.
   c) Bei der Zellatmung entstehen zwei Gase, welche ausgeatmet werden. Wie groß ist das entstehende Volumen der ausgeatmeten Stoffe?
   d) Ein erwachsener Mensch atmet pro Tag ca. 500,00l Kohlenstoffdioxid aus. Welche Masse hat dieses Gasvolumen?
5. Es sollen 10ml Salzsäure (enthalten n= 0,001 mol/l) mit Kalkwasser neutralisiert werden. (Kalkwasser ist eine wässrige Lösung von Calciumhydroxid).
   a) Berechne die notwendige Stoffmenge in mol an Calciumhydroxid, die notwendig ist.
   b) Wie viel Calciumcarbonat muss zur Herstellung der notwendigen Menge Calciumhydroxid abgewogen werden?
   c) Welche Produkte entstehen?
6. Aus 10,00l Wasserstoffgas und 10,00l Chlorgas entsteht bei einer Reaktion Chlorwasserstoffgas. Aber wie viel Liter entstehen?
7. Ein unbekanntes Gas wird im Labor untersucht. Durch Vergleiche und eine sehr feine Waage bestimmt man die Dichte bei Normalbedingungen mit 0,00196 g/cm³. Bestimme die molare Masse und so den Namen des Gases.
8. Welches Volumen benötigen 3,222 mol eines Gases unter Normbedingungen?
9. In einem Versuch wird gemessen, dass eine Stoffportion eines unbekannten Stoffes mit der Masse 1,52 g eine Stoffmenge von 0,033 mol enthält. Um welchen Stoff handelt es sich?
10. Bestimme die Stoffmenge, welche in 3,13 g Glykol (C₂H₆O₂) enthalten sind. Dann berechne die Anzahl an den Atomen C, H und O in 3,13 g Glykol?
11. Bestimme die Stoffmenge und die Anzahl an Molekülen, welche in 3,75g eines 75% Schwefelsäure (H₂SO₄) enthalten sind.
12. Eisensulfid entsteht, wie Du ja noch weißt, durch die Vereinigung von Eisen und Schwefel. Dabei sollte theoretisch für jedes Atom Eisen auch ein Atom Schwefel vorhanden sein. Wenn man nun aber 11,2g Eisen verwendet und eine unbekannte Menge Schwefel vorliegt und man so nur 5,4g Eisensulfid erhält, dann war nicht genügend Schwefel vorhanden. Wie groß ist in diesem Fall die Ausbeute an
13. Eisensulfid in Prozent der theoretisch möglichen Ausbeute?
    a) 75 %
    b) 54 %
    c) 48 %
    d) 31 %
    e) 25 %
14. Welche der folgenden Aussagen ist nicht richtig? (Tipp: 1l = 0,001m³)
    0,2 m³ Sauerstoff unter Standardbedingungen (Vm = 24,8 l/mol!)
15. a) wiegen 258g.
16. b) kann man aus 1000l Luft herstellen.
17. c) enthalten rund 9,7 · 10²⁴ Sauerstoffatome.
18. d) benötigen genau 16,3g Wasserstoff um damit vollständig zu Wasser zu reagieren.
19. e) haben eine Dichte von 1,3· 10^–3 g/cm³.

 

Übersicht über die Messgrößen und ihre Maßeinheiten

Messgröße	Symbol	Einheit
Masse	m	g (kg)
Volumen	V	l
Dichte	ρ	g/ml
Stoffmengea)	n	mol
molare Masseb)	M	g/mol
Konzentration = Molarität	c	mol/l
Energie	E	J = kg·m2/s2
Energie (früher, aber noch gebräuchlich)	E	Kalorie, 1 cal entspricht 1.484 J
Energie (im atomaren Bereich)	E	1 eV entspricht 1.6·10-19J
Reaktions-Enthalpie	ΔH	kJ/mol
(absolute) Temperatur	T	K
Reaktions-Entropie	ΔS	kJ/mol·K
Druck	P	Pa = N/m2
Druck (früher, aber noch gebräuchlich)	Bar	1 bar = 105 Pa
Ladung	C	Coulomb

Die Gasgesetze: Spezialfälle der allgemeinen Gasgleichung (Oberstufe)

Es gibt verschiedene Spezialfälle des allgemeinen Gasgesetzes, welche einen Zusammenhang zwischen zwei Größen herstellen, während alle anderen Größen konstant gehalten werden. Erklärt und nicht nur empirisch abgeleitet werden diese Zusammenhänge zwischen den Zustandsgrößen eines Gases durch dessen Teilchencharakter, also durch die kinetische Gastheorie.

 

a) Gesetz von Boyle-Mariotte

Unabhängig voneinander haben der irische Physiker Iren Robert Boyle (1662) und der Franzose Edme Mariotte (1676) dieses Gesetz formuliert.

Dieses Gesetz sagt aus, dass der Druck idealer Gase bei gleichbleibender Temperatur und gleichbleibender Stoffmenge umgekehrt proportional zum Volumen ist.

Würde man also den Druck auf eine bestimmte vorher festgelegt Menge Gas erhöhen, wird das Volumen entsprechend verkleinert. Umgekehrt sorgt eine Verringerung des Drucks für eine Ausdehnung des Gases, also eine Vergrößerung des Volumens.

 

Für T = konstant sowie n = konstant gilt:

          1                                          p₁       V₂
p ~ ——— => p · V = konstant => —— = ———
          V                                         p₂        V₁

 

b) Gesetz von Gay-Lussac

Jacques Charles (1787) und Joseph Louis Gay-Lussac (1802) beschrieben in diesem Gesetz, dass das Volumen idealer Gase bei gleichbleibendem Druck und gleichbleibender Stoffmenge direkt proportional zur Temperatur ist.

Somit dehnt sich ein Gas bei einer Erhöhung der Temperatur aus und verringert sein Volumen bei Abkühlung. Dieser Zusammenhang wurde erkannt.

 

Für p = konstant und n = konstant gilt:

                V                            V₁      T₁
T ~ V => —— = konstant => —— = ———
                T                           V₂      T₂

 

Zusatzinformationen:

• https://de.wikipedia.org/wiki/Gasgesetz
• https://de.wikipedia.org/wiki/Universelle_Gaskonstante

 

c) Das allgemeine Gasgesetz

Fasst man die bisherigen Gasgesetze in einer Gleichung zusammen, so erhält man die thermische Zustandsgleichung idealer Gase, welche auch allgemeines Gasgesetz bezeichnet wird. Obwohl es sich bei diesem Gesetz nur um eine Näherung handelt, ist sie in ihren Ergebnissen doch sehr präzise!

Aus dieser allgemeinen Gasgleichung sagt somit auch aus, dass die Innere Energie eines Idealen Gases unabhängig von Druck und Volumen ist und somit nur von der Temperatur abhängt! (Also aus der kinetischen Energie der Eigen- und Wärmebewegung der Moleküle!)

 

Extensive Form des allgemeinen Gasgesetzes:

p · V = n · R_m · T

 

Intensive Form des allgemeinen Gasgesetzes:

p · V_M = R_m · T

 

R_m - universelle oder molare Gaskonstante = 8,314472 J / (mol · K)

V_M - molares Volumen

n - Stoffmenge

 

Die Arrheniusgleichung (Oberstufe)

Die Arrhenius-Gleichung wurde von dem finnischen Physiker Svante Arrhenius aufgestellt. Sie beschreibt die Abhängigkeit der Reaktionsgeschwindigkeitskonstante k von der Temperatur.

k = A · e ^{(-E_A / R·T)}

 

A = präexponentieller Faktor (bzw. Frequenzfaktor), welcher nach der Stoßtheorie dem Produkt aus der Stoßzahl Z und dem Orientierungsfaktor P entspricht.

E_A = Aktivierungsenergie in [J/mol]

e = 2,718281828459... (Eulersche Zahl)

R = 8,314 J/(K mol) (allgemeine Gaskonstante)

T = absolute Temperatur [K]

k = Reaktionsgeschwindigkeitskonstante

 

Eine wesentliche Aussage dieser Gleichung, die auch durch die RGT-Regel bestätigt wird, ist, dass die Reaktionsgeschwindigkeit mit ansteigender Temperatur zunimmt.

 

Zusatzinformationen:

https://de.wikipedia.org/wiki/Gasgesetz

https://de.wikipedia.org/wiki/Universelle_Gaskonstante

Auch diese Gleichung ist nicht 100%ig exakt (vor allem, weil A minimal temperaturabhängig ist). Sie ist aber eine sehr gute Näherung!

 

Weitere Aufgaben:

Viele weitere Aufgaben findest Du in den Kapiteln der Oberstufe. Vor allem in den Kapiteln zum chemischen Gleichgewicht, zum Löslichkeitsgleichgewicht und zur Säure-Base Chemie

Fußnoten: