Kapitel 19: Das Orbitalmodell als Atommodell

Der historische Weg zum Orbitalmodell
Zu Beginn des 20. Jahrhunderts wurde in Deutschland, vor allem in Göttingen, versucht den Aufbau von Atomen und die Bewegung der Elektronen zu verstehen. Es gab zu Beginn des Jahrhunderts zuerst das Atommodell von Niels Bohr, welches aber wichtige Fragen unbeantwortet ließ.
Physiker Albert Einstein, Werner Heisenberg, Erwin Schrödinger, Pauli und viele mehr haben versucht durch ihre Forschungen und theoretischen Überlegungen ein universell gültiges Atommodell zu schaffen. So entstand nach und nach ein neuer Zweig der Physik, die Quantenmechanik.
Zur Quantenmechanik, die die klassische Physik erweiterte, entstand auch das Orbitalmodell, ein Atommodell, welches zwar komplexer als das bisherige Bohr‘sche Atommodell war, aber inhaltlich keine Widersprüche aufwies und so wichtige Fragen der Physik klären konnte.
Das Orbitalmodell hat einen sehr komplexen mathematischen Hintergrund. Es basiert auf der Schrödingergleichung, welche frühestens im universitären Chemie- oder Physik-Studium behandelt wird. Hier wird auf diese Hintergründe im folgenden nicht eingegangen.
Die folgenden Seiten fassen den historischen Weg und die Überlegungen zusammen, die zuerst zum Bohr‘schen Atommodell und dann schließlich zum Orbitalmodell führten.
Das Bohr‘sche Atommodell (1913)
Analysiert man die Flammenfarbe von Wasserstoff und leitet das Licht durch ein Prisma, welches das Licht in Einzelfarben zerlegt. So sieht man das charakteristische Farbspektrum, welches in Form eines Linienspektrums sichtbar wird.
Niels Bohr nutze solche Spektren, um Aussagen über den Energiezustand von Elektronen zu treffen. Aus den gewonnenen Linienspektren verschiedener Elemente erstellte er sein nach ihm benanntes Atommodell, 1913.
Elektronensprünge von angeregten Zuständen auf den Zustand n=2 emittieren Strahlung
Beim Wasserstoff umfasst das Gesamtspektrum 5 Serien. Die Balmerserie ist eine davon. Sie liegt im sichtbaren Bereich:

Lichtemmissionen führen zum Linienspektrum
Für Sprünge, die auf N=2 enden, findet Lichtemiision statt (Balmer-Serie). Durch diese Linienspektren kam dem Aufenthaltsbereich etwas näher! Beim Wasserstoffspektrum werden fünf Serien nach dem jeweiligen Wechsel eines Elektrons auf die höher liegenden Schalen unterschieden:
-
Lyman-Serie (UV) Sprünge auf die K-Schale (n = 1)
-
Balmer-Serie (Vis) Sprünge auf die L-Schale (n = 2)
-
Paschen-Serie (IR) Sprünge auf die M-Schale (n = 3)
-
Brackett-Serie (IR) Sprünge auf die N-Schale (n = 4)
-
Pfund-Serie (MW) Sprünge auf die O-Schale (n = 5)
=> Die Linienspektren spiegeln also die verschiedenen möglichen Energiezustände des Wasserstoffatoms wider und verhalfen somit zu einem Abbild der Struktur der Atomhülle.
Niels Bohr stellte folgende Hypothesen auf:
1. Elektronen umkreisen auf Bahnen den Atomkern. Diese Bahnen nannte er Schalen. Die Bewegung benötigt keine Energie und alles passiert ohne Energieverlust.
2. Elektronen können unterschiedliche Schalen, mit verschiedenen Abständen zum Kern besetzen. Jede Schale entspricht einer bestimmten Energie. Die inneren Schalen haben dabei ein geringes Energieniveau. Jede weitere Schale hat dann jeweils ein höheres Energieniveau als die darunterliegenden Schalen.
Elektronen auf der innersten Schale kommt also die geringste Energie zu.
3. Fügt man einem Atom Energie zu, verlässt das Elektron seine Schale und springt auf eine höher liegende Schale (er sprach auch vom Wechsel des Elektrons vom Grundzustand in den angeregten Zustand. Die Energiezufuhr nannte er auch „Anregung“). Diese Energie zum Wechsel der Schale auf ein höheres Energieniveau ist notwendig, da die elektrostatische Anziehungskraft des positiven Atomkerns überwunden werden muss.
4. Kehrt das Elektron dann wieder in einen tiefer liegenden Zustand zurück, wird die vorher aufgenommene Energie abgeben (= emittiert). Die Energieabgabe kann z.B. durch Lichtabgabe erfolgen. Dieses Licht hat er mit seinem oben beschriebenem Versuch gemessen und die Energiedifferenzen zwischen den einzelnen Zuständen den einzelnen Bahnen zugeordnet.
5. Die Schalen bezeichnete Bohr auch als Hauptquantenzahlen. Dafür verwendete er auch den Buchstaben „n“. Die erste Schale hat somit die Hauptquantenzahl n=1, die zweite n=2 usw… Der Wert kann nur ganzzahlige Werte aus den natürlichen Zahlen einnehmen (1-8).
Hin und wieder werden die Schalen auch durch einzelne Buchstaben benannt (das verwirrt aber oft nur).

Die Bohr‘schen Schalennummer entspricht der Hauptquantenzahl
Erweiterung des Bohrschen Atommodells durch Sommerfeld
Sommerfeld übernahm Bohrs Hauptquantenzahl „n“. Diese gibt das „Hauptenergieniveau“ eines Elektrons an. Er fand aber heraus, dass die Energieniveaus innerhalb einer Schale nicht immer einheitlich waren.
Daraufhin definierte er „Unterbahnen“ (also Energie-Unterniveaus) und führte so die Nebenquantenzahl „l“ (kleines L) ein.
„l“ kann Werte von 0 (später s-Elektronen genannt), 1 (später p-Elektronen), 2 (später d-Elektronen), 3 (später f-Elektronen) bis maximal n-1 annehmen.
Eine Erweiterung des Modells wurde notwendig: Wo befindet sich das Elektron nun genau?
Während sich der Aufbau des Atomkerns aus Protonen und Neutronen in den Modellen von Bohr und dem Orbitalmodell nicht unterscheiden, so liegt doch ein großer Unterschied hinsichtlich des Aufenthaltsbereichs der Elektronen vor. An diesem Punkt hatte Bohr zwar wichtige Dinge herausgefunden, aber das Schalenmodell erklärte vieles nicht. Selbst Bohr hatte sich nach wenigen Jahren schon davon distanziert.
Die „De-Broglie-Gleichung“ (1924) und das Welle-Teilchen Dilemma
Der französische Physiker Louis De Broglie stellte 1924 eine Gleichung auf, wonach alle Teilchen eine bestimmte Wellenlänge besitzen, die vom momentanen Impuls des Teilchens abhängig ist (Impuls = m ·ν). Dies gilt auch für Elektronen.
h
λ = ————
m · ν
h = Planksche Konstante, h = 6,62608 · 10–34 J·s
λ = Wellenlänge
ν = Frequenz
Damit bewies De Broglie, dass jedes Teilchen gleichzeitig auch Eigenschaften von Wellen aufweist. Man spricht somit auch vom Welle-Teilchen-Dualismus.
Zusatzinformationen:
Frequenz und Wellenlänge stehen übrigens durch die Lichtgeschwindigkeit, mit der sich elektromagnetische Strahlen ausbreiten, miteinander in Beziehung:
c = ν · λ
c = 2,9979 · 108 m/s
Heisenbergs Unschärferelation (1927)
Heisenberg (1901-1976) postulierte 1927 in seiner Aussage zur Unschärferelation, dass man bei kleinen Teilchen, wie z.B. den Elektronen, nicht gleichzeitig Position und Energie (also z.B. die Geschwindigkeit) bestimmen kann. Dies stand im Widerspruch zu Bohrs Atomtheorie und verlangte ein neues Atommodell!
Zum Vergleich: Möchte man die Geschwindigkeit eines fahrenden Autos messen, kann man dies nicht mit einem Foto machen. Das Foto verrät nur den genauen Ort zu einer bestimmten Zeit. Um eine Geschwindigkeit zu messen, braucht man eine bestimmte Strecke, die das Auto fährt und somit zwei Messpunkte.
Diese erst einmal recht simple Tatsache stellt die Physik aber vor ein großes Problem, da es immer schwieriger wird, Aussagen zu Ort und Geschwindigkeit zu verallgemeinern, je kleiner Teilchen werden. Bedenke, Elektronen sind ca. um den Faktor 1000 kleiner als Protonen und Neutronen.
Während also Niels Bohr in seinem Atommodell noch fest definierte Schalen als Aufenthaltsort postulierte, sprach Heisenberg nun von Aufenthaltsbereichen, und Aufenthaltswahrscheinlichkeiten, das heißt Orten, wo sich das Elektron mit einer hohen Wahrscheinlichkeit befindet. Eine genaue Ortsbestimmung ist hingegen nicht möglich!
Zwei Vergleiche zur Veranschaulichung:
-
Ein Torwart befindet sich während der Halbzeit eines Fußballspiels überwiegend vor dem Tor und vermutlich zu 95% der Zeit im eigenen Strafraum. Diesen kann er aber verlassen, eine feste Grenze liegt nicht vor.
-
Motten und andere Nachtfalter werden nachts von leuchtenden Lampen angezogen und umfliegen diese.
Für beide Beispiele gilt, dass man nicht genau vorhersagen kann, wo sich der Torwart oder die Motte zu einem bestimmten Zeitpunkt befindet, aber ihr ungefährer Aufenthaltsbereich kann mit großer Wahrscheinlichkeit vorhergesagt werden.
Die Schrödingergleichung und das Welle-Teilchen Dilemma
Nun stellt sich die Frage, nach den Bereichen der Aufenthaltswahrscheinlichkeiten der Elektronen. Wenn man nach Heisenberg die Position und die Geschwindigkeit nicht bestimmen kann, dann kann man sie vielleicht berechnen?
Der österreichische Physiker Erwin Schrödinger berechnete dann in seinen Schrödinger-Gleichungen, die Zustände von Elektronen. Die Energiezustände der Elektronen entsprechen in den Gleichungen „stehenden“ Wellen. Diese Wellen haben alle gemeinsam, dass sie in ihrer Funktion von „Null“ auf einen Maximalwert ansteigen und dann wieder den Wert Null annehmen.
Siehe auch Animation der stehenden Welle bei Wikipedia: https://de.wikipedia.org/wiki/Stehende_Welle#/media/Datei:Standing_wave_2.gif
Diese Nullstellen werden als Knoten bezeichnet, der Ausschlag nach oben wird mit + bezeichnet, der nach unten mit –. Die berechneten Lösungen der Schrödingergleichungen nannte er „Wellenfunktion“. Sie werden mit dem griechischen Buchstaben psi ψ bezeichnet. Der berechnete Wert ψ ist aber keiner Eigenschaften der Atome.
Das Quadrat der Wellenfunktion (ψ2) hingegen gibt die Wahrscheinlichkeit an, ein Elektron zu einem bestimmten Zeitpunkt anzutreffen. Ψ2 gibt ebenfalls die Ladungsdichte des Elektrons an, sie beträgt „Null“ an den Knotenflächen. Diese Werte der Aufenthaltswahrscheinlichkeiten werden auch als Atomorbitale bezeichnet.
Die Orte an denen sich Elektronen mit hoher (95%iger) Aufenthaltswahrscheinlichkeit befinden, werden Orbitale genannt. Man kann sich diese Bereiche oft als Kugeln oder Hanteln vorstellen (allerdings ohne feste Grenze!), in denen sich das Elektron frei bewegt.
Die Quantenzahlen beschreiben die Elektronen in ihren Orbitalen
Jedes Orbital in einem Atom wird genau durch vier Quantenzahlen beschrieben. Diese sind in ihren Bezeichnungen zum Teil von Bohr übernommen worden.
-
Die Hauptquantenzahl [n] entspricht der Schale im Bohr‘schen Atommodell.
-
Die Nebenquantenzahl [l] (kleines L) gibt die Unterteilung der Schalen in „Unterschalen“ an. „l“ kann Werte von 0 (s-Elektronen genannt), 1 (p-Elektronen), 2 (d-Elektronen), 3 (f-Elektronen) bis maximal n-1 annehmen. Die Buchstaben s, p, d, f haben sich anstelle der Nummern etabliert und werden heute fast ausschließlich als Namen für die jeweiligen Orbitale verwendet.
(Die Buchstaben der Orbitalbezeichnungen (auch Symbole genannt) leiten sich übrigens von den englischen Adjektiven, mit denen die Spektrallinien bezeichnet werden, ab:
s von sharp, p von principal, d von diffuse, f von fundamental). -
Die Magnetquantenzahl [m] gibt die Orientierung des Orbitals an. Sie ist definiert von -1 bis 1.
-
Die Spinquantenzahl [s] gibt den Spin des Elektrons an, also die Drehung um die eigene Achse. Es gibt dabei zwei Spinrichtungen, welche mit den Zahlen - ½ und + ½ angegeben werden.
Das Pauli-Prinzip
Der Physiker Pauli fügte diesem Modell noch die Aussage zu, dass in einem Atom niemals zwei Elektronen komplett die gleichen Quantenzahlen haben können, sie müssen sich mindestens in einer unterscheiden. Möchte man also die Elektronenkonfiguration eines Atoms aufstellen und beschreiben, so werden die Orbitale mit niedrigem Energieniveau zuerst besetzt werden, dann die mit höherem:
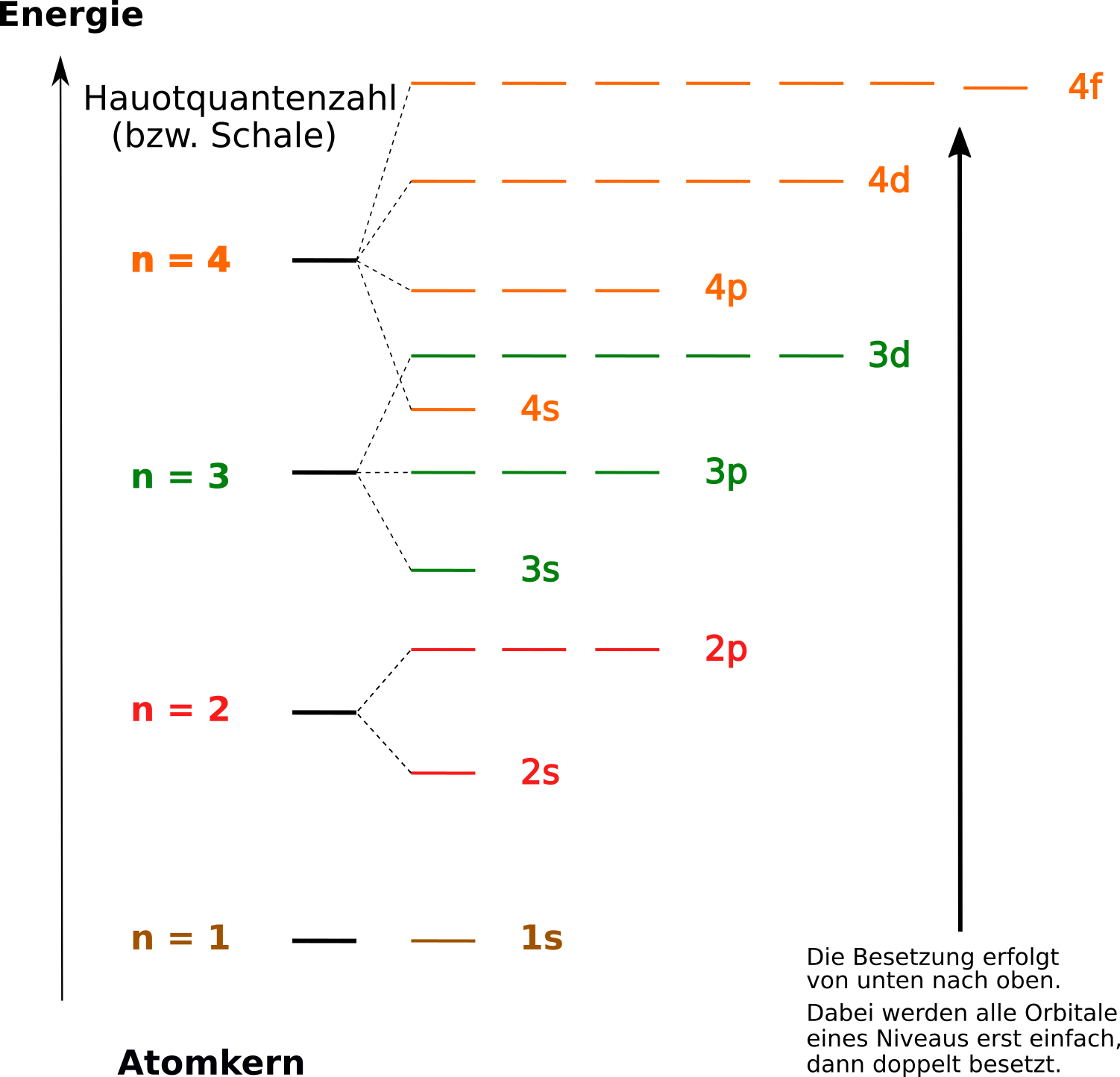
Siehe dazu auch die Beispiele auf der nächsten Seite.
Die Hund‘sche Regel
Der Physiker Hund fügte nach Pauli nun noch eine weitere Regel hinzu. Er bemerkte, dass es immer mehrere Orbitale gibt, die das gleiche Energieniveau haben. Er nannte diese auch entartete Orbitale. Wenn also Orbitale des gleichen Energieniveaus besetzt werden, dann werden sie zuerst nur mit einem Elektron besetzt. (Hund‘sche-Regel).
Hund stellte dabei ebenfalls fest, dass wenn ungepaarte Elektronen vorliegen, diese in ein Magnetfeld hineingezogen werden (paramagnetische Substanzen). Die Stärke des Magnetismus hängt von der Anzahl an ungepaarten Elektronen ab. Diamagnetische Substanzen hingegen werden von einem Magnetfeld schwach abgestoßen, da alle Elektronen gepaart sind.
a) Beispiele zur Besetzung: Wasserstoff & Sauerstoff

Wasserstoff

Sauerstoff
b) Beispiele zur Besetzung: Magnesium, Eisen & Brom

Magnesium

Eisen

Brom
Mit diesen Regeln im Kopf, kann die Besetzung verkürzt in der Form wiedergegeben werden, dass man die Konfiguration des höchsten Energieniveaus angibt (siehe jeweils oben in den Grafiken). Hochgestellte Zahlen geben die Anzahl an Elektronen wieder: Sauerstoff => 3s23p4.
Das Periodensystem spiegelt in seinem Aufbau dies nun wider. Die Hauptgruppen 1 und 2 haben das s-Orbital besetzt, die Hauptgruppen 3-8 besetzten zusätzlich die p-Orbitale.
In den Nebengruppen werden zusätzlich die d-Orbitale besetzt. Lanthanoide und Actinoide besetzten ebenfalls die f-Orbitale.
Edelgase haben die Elektronenkonfiguration: ns2np6.
Formen der Atomorbitale
Orbitale haben eine charakteristische Form. Von Energieniveau zu Energieniveau kommen neue hinzu. Sie unterscheiden sich oft deutlich!
s- und p-Orbitale

Public domain by Wikicommonsuser Benjah-bmm27; Thank you; https://commons.wikimedia.org/wiki/File:AOs-3D-dots.png
s-Orbitale im Vergleich

Das Neon-Atom und seine Orbitale

d-Orbitale

Creative Commons Attribution-Share Alike 4.0 International& GNU Free Documentation License, Version 1.2 by wikicommonsuser J3D3, Thank you; https://commons.wikimedia.org/wiki/File:Orbitalesd.JPG
Detaillierte Regeln zur Elektronenverteilung
Jedes Element, außer Wasserstoff, verfügt über mehrere Elektronen. Wie verteilen sich diese nun?
Grob gesagt, passen in ein Orbital nur immer 2 Elektronen. Liegen also viele Elektronen vor, so gibt es auch mehrere „Orbitalkugeln“.
1. Anzahl der Orbitale (Hauptquantenzahl) und der Spin
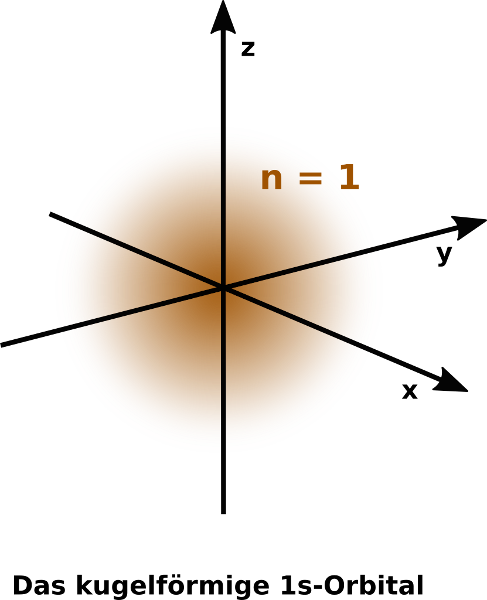
Da jedes Orbital nur Platz für zwei Elektronen hat, haben also die Elemente der 1. Periode (H, He) nur ein Orbital, da mehr als 2 Elektronen nicht vorkommen. Dieses (erste) Orbital wird „1s“ genannt (die 1 steht dabei für die Periodennummer und der Buchstabe s für die Form des Orbitals. Die Elemente der zweiten Periode können maximal 8 Elektronen haben, demzufolge liegen maximal vier Orbitale vor: 2s, 2px, 2py, 2pz
Beachte: s-Orbitale sind Kugelförmig, p-Orbitale sind hantelförmig. Diese Hanteln kann man sich wie die drei Achsen (x,y und z) eines dreidimensionalen Koordinatensystems vorstellen, weswegen die Buchstaben x,y und z oft zugefügt werden (s.o.).
Elemente der dritten Periode können maximal 18 Elektronen haben, demzufolge gibt es das 3s-Orbital, drei 3p-Orbitale und fünf 3d-Orbitale.
Beachte: das 1s-Orbital ist dabei etwas kleiner als das 2s-Orbital, welches wiederum kleiner als das 3s-Orbital ist.
Merke: s-Orbitale sind einfach, p-Orbitale sind dreifach, d-Orbitale sind fünffach und f-Orbitale sind siebenfach.
Wie unterscheiden sich nun die beiden Elektronen in einem Orbital?
Sind in einem Orbital nun zwei Elektronen vorhanden, so haben sie eine unterschiedliche, entgegengesetzte Bewegungsrichtung. Man spricht auch vom unterschiedlichen Spin.
Die Quantenzahlen
Jedes Elektron eines Atoms ist nun genau durch Quantenzahlen beschreibbar. Keine zwei Elektronen sind gleich. Die Quantenzahlen geben nun das Orbital, den Spin und vieles mehr an. Im Grunde geben sie damit auch den Energiezustand wieder.
Insgesamt kann jedes Elektron durch vier Quantenzahlen charakterisiert werden:
1. Die Hauptquantenzahl „n“ (natürlich Zahl: 1, 2, 3, 4 usw.) entspricht der Periodennummer, also der Schale nach dem Bohr‘schen Atommodell.
Wie auch im Bohr‘schen Atommodell gilt im Orbitalmodell: Je größer n ist, desto weiter ist das Elektron vom Atomkern entfernt und desto größer ist der Radius des Atoms.
Perioden:
n = 1 Wasserstoff und Helium
n = 2 Lithium bis Neon
n = 3 Natrium bis Argon
n = 4 Kalium bis Krypton (sowie Scandium bis Zink)
n = 5 Rubidium bis Xenon (sowie Yttrium bis Cadmium)
n = 6 Cäsium bis Radon (sowie Lanthan bis Quecksilber & Cer bis Luthetium)
n = 7 Francium und Radium (sowie Actinium bis Lawrencium & Rutherfordium bis Element 118)
2. Die Nebenquantenzahl „l“ (ganze Zahl von 0, 1, 2 usw. bis n-1) beschreibt die Form des jeweiligen Orbitals und ist ebenso ein Maß für den Drehimpuls des Elektrons.
3. Die Magnetquantenzahl „m“ (ganze Zahl zwischen -l bis +l ist) beschreibt die räumliche Ausrichtung, die das Orbital bezüglich eines äußeren Magnetfeldes einnimmt. Demzufolge ist diese Zahl auch nur messbar, wenn von außen ein Magnetfeld angelegt wird.
4. Die Spinquantenzahl (+ 0,5 oder -0,5 ist, bzw. +½ () oder -½ ()) gibt die Bewegungsrichtung eines Elektrons an. Dabei gibt es nur zwei mögliche Zustände.
Regeln zur Besetzung der Elektronen
Die Besetzung der Orbitale, also die Verteilung und Zuordnung der Elektronen geschieht natürlich nicht zufällig, sie folgt festen Regeln.
1. Aufbauprinzip:
Die Elektronen besetzten zuerst die energetisch niedrigsten Orbitale
2. Hundsche Regel:
Orbitale eines Typs (also z.B. die 2p-Orbitale) werden zuerst einzeln besetzt. Zum Beispiel im Falle des p-Orbitals werden zuerst die ersten drei Elektronen in je ein Orbital gesetzt. Diese Elektronen haben dann auch den gleichen Spinzustand. Sind alle Orbitale eines Niveaus besetzt, so kommt es zur Paarung mit entgegengesetztem Spin.
3. Pauli-Prinzip / Pauli Verbot:
Elektronen müssen sich mindestens in einer der vier Quantenzahlen unterscheiden!
=> Jedes Elektron hat also eine eigene Quantenzahlfolge.
Tipps:
-
Ein Element kann maximal 2n2 Elektronen besitzen (n= Periodennummer).
-
Sind die höchsten d-Orbitale voll besetzt (also die der äußeren Elektronenhülle), spricht man von Edelgas-, bzw. Valenzelektronen-Konfiguration.
-
Es gibt 18 Gruppen.
-
Jede neue Periode beginnt, wenn die vorherige innerhalb ihres Hauptenergie-Niveaus vollständig mit Elektronen besetzt ist.
-
Die Nummerierung der Perioden entspricht der Hauptquantenzahl n.
Die 18 Gruppen des PSE, ihre Namen und die Edelgaskonfiguration
1 ns1 Alkalimetalle (Li bis Fr)
2 ns2 Erdalkalimetalle (Be bis Ra)
3 ns2(n-1)d1 Scandiumgruppe (Sc, Y, La, Ac; n = 4, 5, 6, 7)
ns2(n-1)d1(n-2)f1-14 n = 6: Lanthanide; n = 7: Actinide
4 ns2(n-1)d2 Titangruppe (Ti, Zr, Nb, Hf, Rf)
5 ns2(n-1)d3 Vanadiumgruppe (V, Nb, Ta, Db)
6 ns1(n-1)d5 Chromgruppe (Cr, Mo, W, Sg)
7 ns2(n-1)d5 Mangangruppe (Mn, Tc, Re, Bh)
8 ns2(n-1)d6 Eisengruppe (Fe, Ru, Os, Hs)
9 ns2(n-1)d7 Cobaltgruppe (Co, Rh, Ir, Mt)
10 ns2(n-1)d8 Nickelgruppe (Ni, Pd, Pt, Rg)
11 ns1(n-1)d10 Kupfergruppe (Münzmetalle; Cu, Ag, Au)
12 ns2(n-1)d10 Zinkgruppe (Zn, Cd, Hg)
13 ns2p1 Bor-Aluminiumgruppe (B bis Tl)
14 ns2p2 Kohlenstoff-Siliziumgruppe (C bis Pb)
15 ns2p3 Stickstoff-Phosphorgruppe (Pnictogene) (N bis Bi)
16 ns2p4 Chalcogene (O bis Po)
17 ns2p5 Halogene (F bis At)
18 ns2p8 Edelgase (He bis Rn)
Im Bohrschen Atommodell gilt die Oktett- oder auch Edelgasregel, nach der voll gefüllte Schalen besonders stabil sind. Das gilt natürlich auch für das Orbitalmodell. Alle Zustände mit gefüllten Energiezuständen (besseres Wort finden) sind recht stabil. Besonders stabil ist der Zustand in dem s- und p-Oribitale ganz gefüllt sind.
Aber auch halb und ganz gefüllten d-Schalen (bei den Gruppen 6 und 11) stellen stabile Zustände mit stabilen Elementen dar.
Hybridisierungen & Hybridorbitale
Beim Kohlenstoff kann man nun etwas besonderes sehen. Er sollte eigentlich eine Elektronenverteilung wie im ersten Bild haben. Tatsächlich hebt sich das s2-Oribital etwas an und die drei 2p Orbitale senken sich ab. Es entstehen neue Orbitale, die eine Mischung sind und eine andere Form haben. Solche Mischorbitale werden Hybridorbitale (Hybrid = Mischling) genannt. Der Vorgang heiß Hybridisierung.

In diesem Fall sind vier sp3-Orbitale entstanden. Kohlenstoff mit dieser Konfiguration ist vierbindig. Alle vier Bindungen sind gleichwertig.

2sp3 - Orbitale sp3 - Bindungswinkel 109,5°

Bindung mit vier Wasserstoffen im Methan CH4
Quelle Bilder: GNU-Lizenz für freie Dokumentation, Version 1.2 sowie Creative-Commons-Lizenz „Namensnennung – Weitergabe unter gleichen Bedingungen 3.0 nicht portiert sowie Creative-Commons-Lizenzen „Namensnennung – Weitergabe unter gleichen Bedingungen 2.5 generisch“, „2.0 generisch“ und „1.0 generisch“ by wikicommonsuser Sven, Thank you; https://commons.wikimedia.org/wiki/File:Sp3-Orbital.svg https://commons.wikimedia.org/wiki/File:Sp2-Orbital.svg https://commons.wikimedia.org/wiki/File:Sp-Orbital.svg?
Quelle Bilde „Ch4_Hybridization“: Public domain by wikicommonsuser K. Aainsqatsi - thank you; https://commons.wikimedia.org/wiki/File:Ch4_hybridization.svg
Es gibt auch sp2-Hybridisierung (dreibindiger Kohlenstoff, mit einer Doppelbindung) und sp- Hybridisierung) (zweibindiger Kohlenstoff mit einer Dreifachbindung).

Sp2 - Orbitale: Bindungswinkel 120°
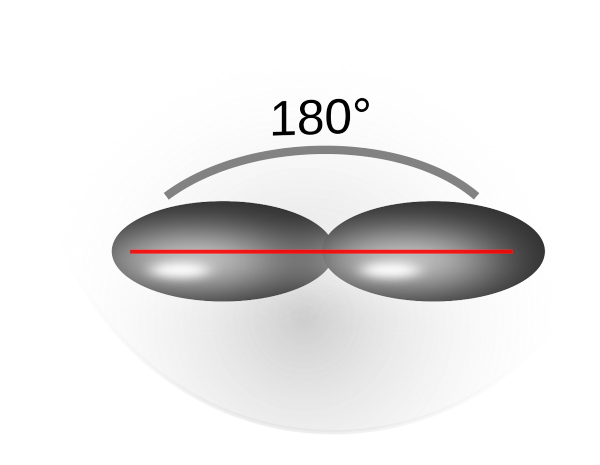
Sp - Orbitale: Bindungswinkel 180°
Linus Pauling, 1931: Hybridorbitale entstehen durch Linearkombination der Wellenfunktionen der grundlegenden Atomorbitale.
Zusatzinformationen: https://de.wikipedia.org/wiki/Hybridorbital
Molekülorbitale und die Molekülorbital-Theorie
Überlappung der Atomorbitale zu Molekülorbitalen
Mithilfe des Orbitalmodells kann nun die Atombindung (=kovalente Bindung) anschaulich und mathematisch durch eine Linearkombination der Elektronen-Besetzungsdiagramme der jeweils an der Bindung beteiligten Atome dargestellt werden.
Dahinter verbirgt sich die Vorstellung, dass die beteiligten Orbitale überlappen und einen großes, gemeinsam genutztes Molekülorbital bilden.
Bilden sich Molekülorbitale so entstehen bindende, energiearme (und somit energetisch stabilisierte) Molekülorbitale sowie antibindende, energiereiche (und somit energetisch instabile Molekülorbitalen. Die antibindenden Molekülorbitale werden mit einem Stern (*) gekennzeichnet.
Man unterscheidet zwischen antibindenden Molekülorbitalen (die Aufenthaltswahrscheinlichkeit zwischen den beiden Atomen ist für Elektronen Null => keine Bindung) und bindenden Molekülorbitalen (maximale Aufenthaltswahrscheinlichkeit zwischen den Bindungspartnern => hohe Elektronendichte => kovalente -(Atom-)Bindung).
Kommt ein bindendenes Molekülorbital durch das Überlappen von zwei s-Orbitalen zustande, so entsteht ein σ-Orbital (Sigma-Orbital) mit einer sogenannten σ-Bindung. Es liegt damit eine Einfachbindung vor (wie z.B. bei H2 => H-H).
σ-Bindungen sind rotationssymmetrisch, das heißt, frei drehbar. π-Bindungen sind nicht frei drehbar!
Überlappen p-Orbitale, so entstehen π-Orbitale mit π-Bindungen.
In der Regel bilden sich immer π-Bindungen zusammen mit einer π-Bindung. So entstehen dann im Molekül Doppel- oder Dreifachbindungen. Diese sind nicht frei drehbar!
π-Orbitale bilden sich übrigens auch, wenn px, py mit d-Orbitalen (außer dem d(z2)) überlappen.
Beispiele für die Konstruktion von Molekülorbitalen bei H2 und He:

Wasserstoff
Die bei der H2-Bildung freiwerdende Bindungsenergie aus den freien Wasserstoffatomen beträgt 435 kJ/mol!

Helium
Quelle Bilder: GNU-Lizenz für freie Dokumentation, Version 1.2 sowie Creative-Commons-Lizenz „Namensnennung – Weitergabe unter gleichen Bedingungen 3.0 nicht portiert by wikicommonsuser Phrood - thank you; https://commons.wikimedia.org/wiki/File:Wasserstoff-Orbitale.svg; https://commons.wikimedia.org/wiki/File:Helium-Orbitale.svg